Tag: Geogebra
-

Circles on a Lissajous Curve: Sunday Maths Animations Week 1
I’ve been enjoying making animations in Geogebra recently, and have decided to try publising one every week on YouTube. Here is week 1.
-

Spiky Feathers and Geometric Fish
The astroid curve is an example of a hypocycloid – a curve generated by rotating a fixed point on a small circle around a larger circle. Specifically, it is a hypocycloid with four cusps.
-

Hyperbolic Paraboloid in Matchmakers
For this year’s MathsJam Bakeoff I made a hyperbolic paraboloid out of matchmakers. For anybody who doesn’t know, matchmakers are thin chocolate sticks with crunchy bits, traditionally mint but now available in orange, salted caramel and possibly other flavours. They are delicious even when they are not being used for maths.
-
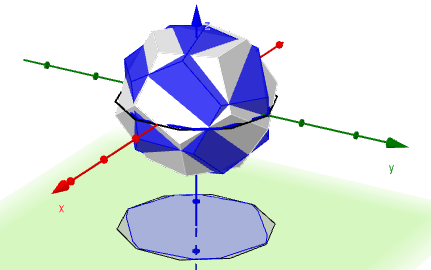
Rupert Polyhedra: Dodecahedron
A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve talked about the Rupert tetrahedron, the Rupert cube and the Rupert octahedron. Today it’s the dodecahedron.
-

Parametric T-shirts
I’m excited to share my new TeeMill site, selling T-shirts based on graphs of parametric equations. There are three designs currently available, and all can be bought in loose fit or fitted, and with or without the equations that created the design displayed underneath. You can also find GeoGebra files, where you can play with…
-

Spin, Laugh and Dance
I’d like to introduce you to the graph of $x=\sin(f_1t)e^{d_1t}$, $y=\sin(f_2t)e^{d_2t}$, a curve that spins, laughs and dances.
-
Cube Shadows
Drag the sliders to rotate the cube and see how its shadow changes.
-

Rupert Polyhedra: Octahedron
A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve already talked about the Rupert tetrahedron and the Rupert cube. Now it’s the turn of the octahedron.
-

Rupert Polyhedra: Cube
Last week, I wrote about Rupert polyhedra, and how a tetrahedron has the Rupert property. The idea dates back to the 1600s, when Prince Rupert of the Rhine won a bet that it was possible to make a hole in a cube that was large enough for an identical cube to pass through, so let’s…
-
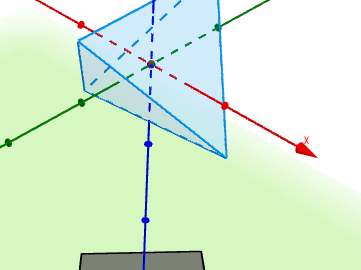
Rupert Polyhedra: Tetrahedron
For a polyhedron to be classed as Rupert, it must be possible to cut a hole in it that is large enough for an identical polyhedron to pass through. It sounds impossible, but many polyhedra have this property, including the tetrahedron.