A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve already talked about the Rupert tetrahedron and the Rupert cube. Now it’s the turn of the octahedron.
In the case of the tetrahedron and the cube, I said that we needed either a shadow that would fit entirely within one face of the solid, or a shadow that could entirely enclose one face. This wasn’t entirely accurate. What we actually need are two shadows, one of which will fit entirely inside the other. So let’s look at the shadows made by an octahedron.
Similarly to the cube, we see squares, rectangles and hexagons, and also some parallelograms. When the octahedron is positioned with every vertex on an axis, its shadow is square. From this position, if it is rotated by $45^\circ$ around the $x$-axis and $\theta=\cos^{-1}\left(\frac{1}{\sqrt{3}}\right)-\cos^{-1}\left(\sqrt\frac{2}{3}\right)$ around the $y$-axis it makes a hexagonal shadow that fits entirely inside the square, as shown below.
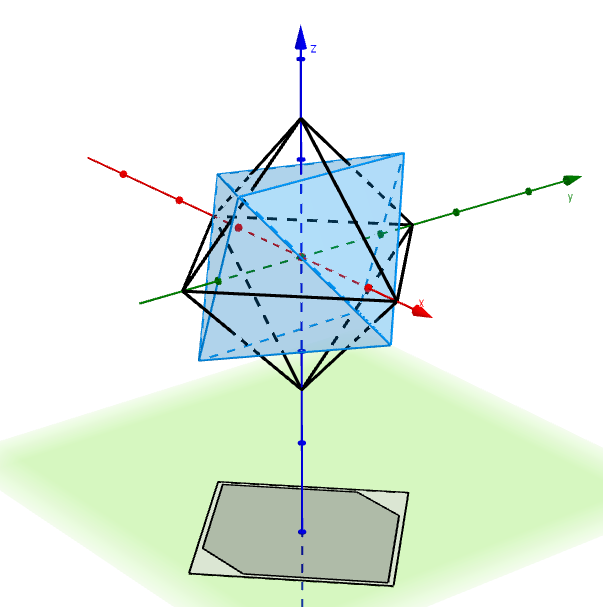
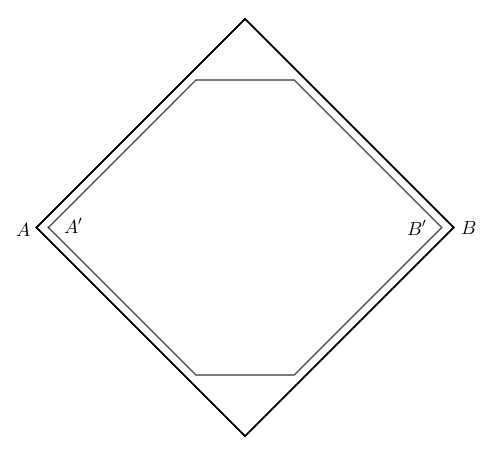
We can calculate the factor by which the octahedron can be scaled, and still fit through the hole (the Nieuwland constant) by finding the ratio of $AB$ to $A’B’$. Assuming that the octahedron has an edge length of $1$, the two points of the original octahedron that sit on the $x$-axis are projected to $A\left(\frac{-1}{\sqrt{2}},0,0\right)$ and $B \left(\frac{1}{\sqrt{2}},0,0\right) $. $A’$ and $B’$ are the projections of these points after the rotations described above.
We can find the coordinates of the corresponding points on the rotated octahedron by applying the rotation matrices
$\begin{pmatrix}
1 & 0 & 0\\
0 & \cos(45) &-\sin(45)\\
0 & \sin(45) &\cos(45)\\
\end{pmatrix}$
and
$\begin{pmatrix}
\cos(\theta) & 0 & \sin(\theta) \\
0 & 1 & 0\\
\sin(\theta) & 0 &\cos(\theta)\\
\end{pmatrix}$
By the magic of cancelling trigonometry (which I invite you to work through yourself) this gives $\left(-\frac{2}{3},0,\frac{1}{3\sqrt{2}}\right)$ and $\left(\frac{2}{3},0,-\frac{1}{3\sqrt{2}}\right)$. Their projections onto the $x$-$y$ plane are $A’=\left(-\frac{2}{3},0,0\right)$ and $B’=\left(\frac{2}{3},0,0\right)$.
So the ratio between the lengths $AB$ and $A’B’$ is
$\begin{align}
\frac{AB}{A’B’}&=\frac{2\left(\frac{1}{\sqrt{2}}\right)}{2\left(\frac{2}{3}\right)}\\
&=\frac{3}{2\sqrt{2}}\\
&\approx 1.06066
\end{align}$
This is the current best estimate for the Nieuwland constant for the octahedron, but it has not been proved to be the biggest. As with the cube, this ratio gives just enough wriggle room to make a 3D-printed version, although there’s not much of the original octahedron left once the tunnel has been cut. You can download the OpenSCAD file from GitHub.
Reference: Most of the information required to write this came from the article Platonic Passages (Jerrard, Wetzel and Yuan, 2017).

Leave a Reply