Last week, I wrote about Rupert polyhedra, and how a tetrahedron has the Rupert property. The idea dates back to the 1600s, when Prince Rupert of the Rhine won a bet that it was possible to make a hole in a cube that was large enough for an identical cube to pass through, so let’s look at how the Rupert property works for a cube.
As with the tetrahedron, we start by looking at the shadows that can be cast by a cube. We’re looking for either a shadow that will fit entirely within one face of the cube, or a shadow that can entirely enclose one face.
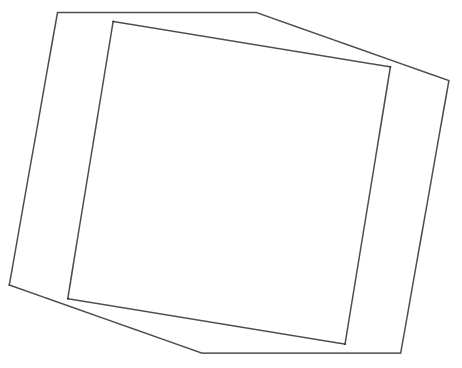
Looking at the shadows, we see squares, rectangles and hexagons.
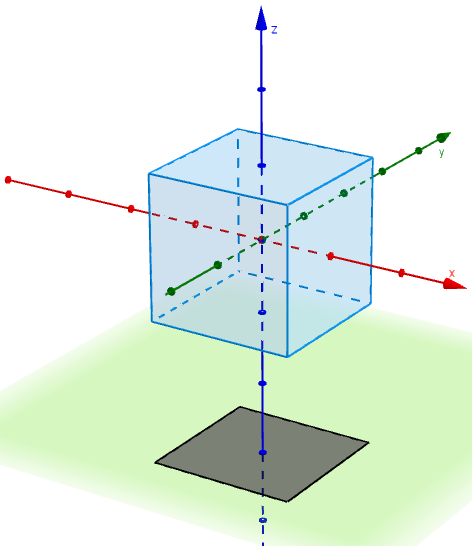
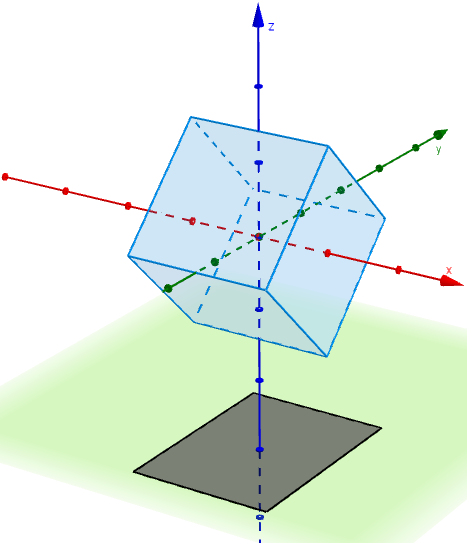
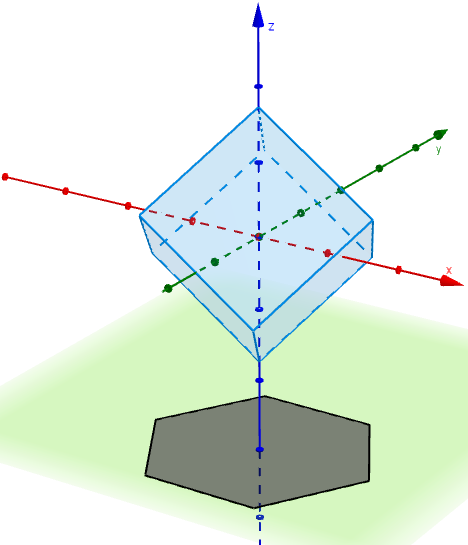
Rotating a cube with side length $1$ by an angle of $45^\circ$ around the $x$-axis and $\cos^{-1}\left(\sqrt{\frac{2}{3}}\right)$ around the $y$-axis produces a shadow that is a regular hexagon, with side length $\sqrt{\frac{2}{3}}$. Will a square of side length $1$ fit inside a hexagon of side length $\sqrt{\frac{2}{3}}$? To work this out, consider a hexagon of side length 1, and work out the maximum size square that will fit inside.
Let $x$ be the length of the side of the square.

Using trigonometry, we know that $\dfrac{d}{\frac{x}{2}} = \tan\left(30^\circ\right)= \dfrac{1}{\sqrt{3}}$. Since the distance from the centre of a regular hexagon to a corner is the same as the side length, we also know that $d+\frac{x}{2}=1\Rightarrow d=1-\frac{x}{2}$. Substitute this value for $d$ into the first equation and rearrange:
$\begin{align}
\frac{1-\frac{x}{2}}{x/2}&=\frac{1}{\sqrt{3}}\\\\
\frac{2-x}{x} &=\frac{1}{\sqrt{3}}\\\\
2\sqrt{3}-\sqrt{3}x&=x\\\\
2\sqrt{3}&=x\left(1+\sqrt{3}\right)\\\\
x&=\frac{2\sqrt{3}}{ 1+\sqrt{3}}\approx 1.267\dots
\end{align}$
So for a hexagon of side length $h$, the largest square that will fit inside has side length $\frac{2\sqrt{3}}{ 1+\sqrt{3}}h$.
The side length of the shadow hexagon is $\sqrt{\frac{2}{3}}$, so the maximum square that will fit inside it has side length
$\begin{align}
\left(\frac{2\sqrt{3}}{ 1+\sqrt{3}}\right)\left(\sqrt{\frac{2}{3}}\right)&=\frac{2\sqrt{2}}{1+\sqrt{3}}\\\\
&\approx 1.035…
\end{align}$
So we can fit a square of side length $1$ inside the shadow and still have a little space left over.
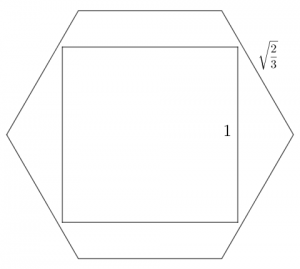
Now imagine extruding that square upwards to make a tunnel through the rotated cube. Because the square fits fully inside the shadow, the tunnel will fit fully inside the cube, producing a cube with the desired size of hole.
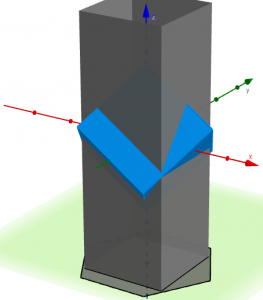
In fact, a slightly different rotation will make a shadow than can contain an even larger square. This was discovered by Pieter Nieuwland, who calculated that for a cube of edge length $1$, the maximum size cube that can fit through a hole has edge length $\frac{3}{4}\sqrt{2}=1.0606\dots$. As I mentioned when talking about the tetrahedron, this number is called the Nieuwland constant – the maximum ratio by which a polyhedron can be increased in size and still fit through a hole in the original-sized polyhedron.
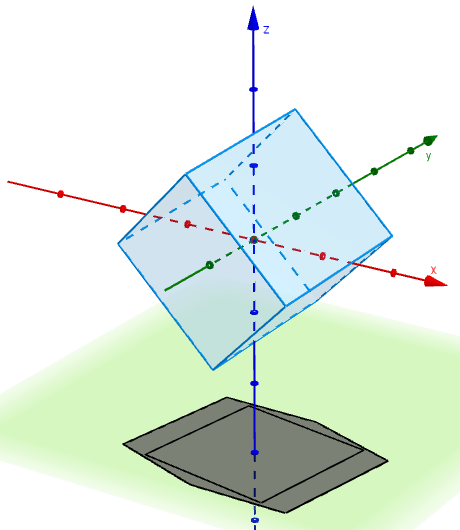
In practice, this slightly larger ratio allows enough wriggle room to make a 3D-printed Rupert cube. You can download the OpenSCAD file for this, as well as the Geogebra file for a rotating cube and its shadow, from GitHub.


Reference: Most of the information required to write this came from the article Platonic Passages (Jerrard, Wetzel and Yuan, 2017).

Leave a Reply