Category: 3D Geometry
-
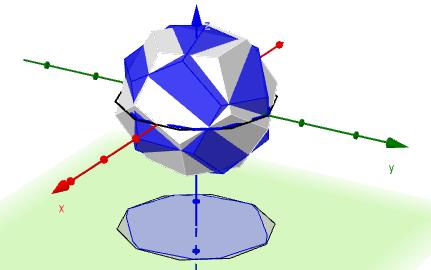
Rupert Polyhedra: Dodecahedron
A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve talked about the Rupert tetrahedron, the Rupert cube and the Rupert octahedron. Today it’s the dodecahedron.
-

The Carpeted Hexaflake
I’m trying to imagine a solid. From the front, it looks like a Koch snowflake. From the top, it looks like a Sierpinski carpet. How might it look from the side? How would it feel? Is it even possible?
-

Rupert Polyhedra: Octahedron
A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve already talked about the Rupert tetrahedron and the Rupert cube. Now it’s the turn of the octahedron.
-

Rupert Polyhedra: Cube
Last week, I wrote about Rupert polyhedra, and how a tetrahedron has the Rupert property. The idea dates back to the 1600s, when Prince Rupert of the Rhine won a bet that it was possible to make a hole in a cube that was large enough for an identical cube to pass through, so let’s…
-
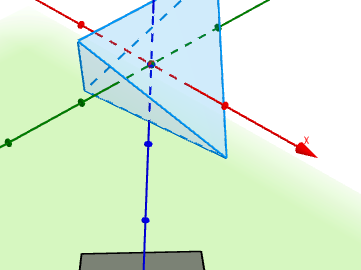
Rupert Polyhedra: Tetrahedron
For a polyhedron to be classed as Rupert, it must be possible to cut a hole in it that is large enough for an identical polyhedron to pass through. It sounds impossible, but many polyhedra have this property, including the tetrahedron.