A polyhedron is Rupert if you can cut a hole in it that’s large enough for an identical polyhedron to fit through. I’ve talked about the Rupert tetrahedron, the Rupert cube and the Rupert octahedron. Today it’s the dodecahedron.

You might remember that if a polyhedron is Rupert, we should be able to find two shadows of the solid, one of which will fit entirely within the other. Use the applet below to rotate the dodecahedron and see what shadows it casts. Download the applet

In the article Platonic Passages, Jerrard, Wetzel and Yuan give a series of rotations that will make the required shadows. I won’t pretend to understand how they worked them out, but will just describe how I implement them here.

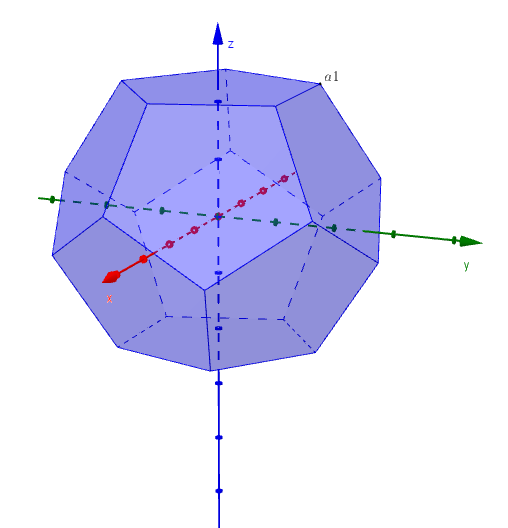
Start with a dodecahedron with its top and bottom face parallel to the $x$-$y$ plane, and centred on the $z$-axis (image a). The projection from above from this position gives the outside shadow. Then perform the following three rotations:

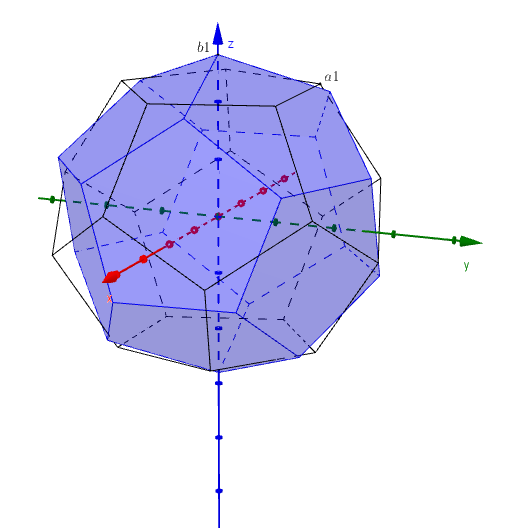
• rotate so that a vertex lies on the $z$-axis (image b)
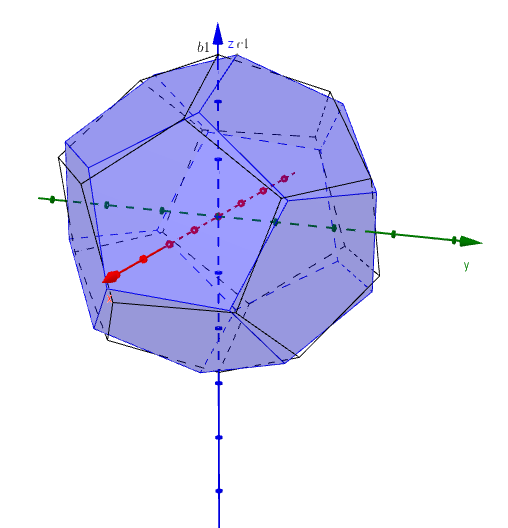
• rotate $6.45^\circ$ about the line $(-1.06,-0.77,0)+(2.12,1.54,0)t$ (image c)
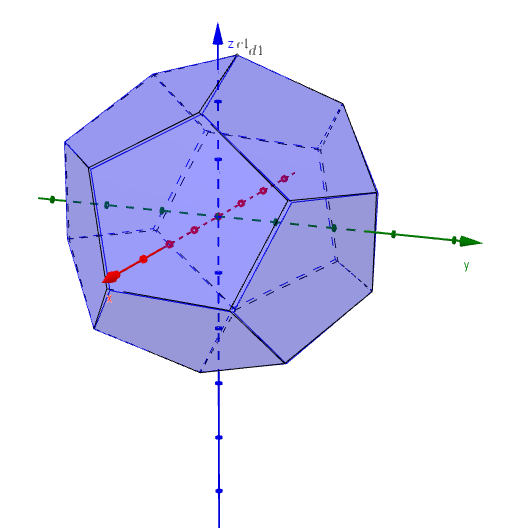
• rotate $1.55^\circ$ about the line $(-0.35,0.49,1.16)+(0.71,-0.97,-2.33)t$ (image d)

The projection from above after the final rotation gives the inside shadow. The lines used in the last two rotations are defined as the lines through the midpoints of particular edges in the article by Jerrard, Wetzel and Yuan.

In each image below, the wire frame shows the previous position of the dodecahedron.

After the third rotation, the shadow will fit entirely inside the original shadow – but only just! The applet below shows the outside (white) and inside (blue) dodecahedra, along with their shadows from above. Verify that one is entirely inside the other by zooming in. (You will have to zoom quite a long way!) Download the applet

I’ve mentioned before that the Nieuwland constant defines how much the size of the inside solid can be increased by and still fit through the outside solid. In other words, how much wriggle room there is. The best-known estimate of the Nieuwland constant for the dodecahedron is $1.005882$, compared to $1.06066$ for the cube and octahedron, and $1.004235$ for the tetrahedron. The smaller this value is, the thinner the narrowest part of the original solid will be after the tunnel is cut. Sadly the value for the dodecahedron is so small that it’s not feasible to build a physical model of the Rupert dodecahedron.