For a polyhedron to be classed as Rupert, it must be possible to cut a hole in it that is large enough for an identical polyhedron to pass through. It sounds impossible, but many polyhedra have this property, including the tetrahedron.

So how is it possible to cut a hole in a tetrahedron that’s big enough for an identical tetrahedron to pass through? To answer this, we have to think about the shadow that a tetrahedron makes. If it can be rotated in such a way that its shadow will fit inside one of its own faces, then the whole thing will fit through a hole cut in that face. Alternatively, if it can be rotated so that one face will fit inside the shadow, then cutting a hole perpendicular to the shadow will do the job.

Let’s start by looking at some of the shadows made by a tetrahedron. The animation below shows a tetrahedron of edge length $1$ rotating around the $x$- and $y$-axes, with its shadow underneath.

There are some triangular shadows and some quadrilateral. Do any of them meet either of the required criteria?

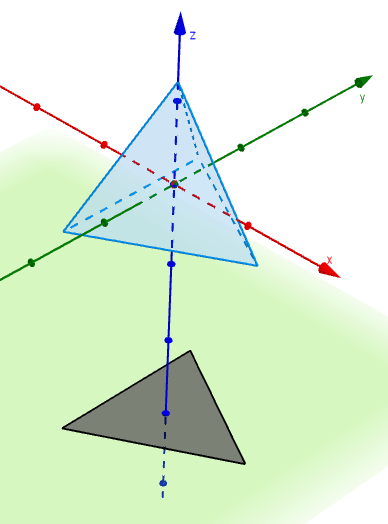
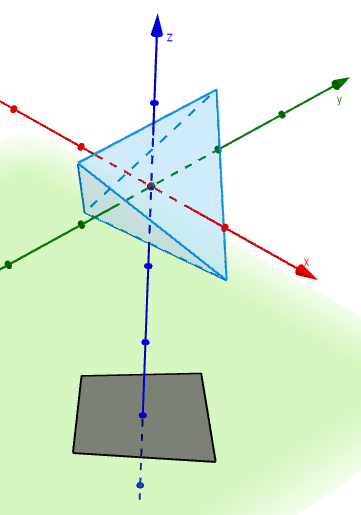
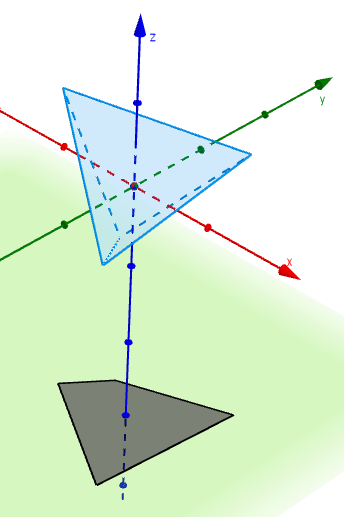
Without going into too many technical details, the tetrahedron can be rotated so that its shadow will fit inside one of the faces. The initial position is as shown in the left-most image above, centred at the origin with the base parallel to the plane $z=0$ and one edge parallel to the $y$-axis. Rotating the tetrahedron by $270^\circ$ around the $x$-axis and $30^\circ + \sin^{-1}\left(\sqrt{6}/3\right)\approx\, 84.736^\circ$ about the $y$-axis gives a triangular shadow that is marginally smaller than the face of the tetrahedron. The next image shows the shadow of the rotated tetrahedron (solid line) inside an equilateral triangle of edge-length $1$ (dashed line).

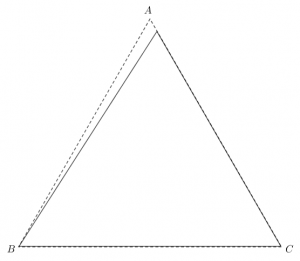
It’s close. To see that it really does fit inside, we need to zoom in on the corners.

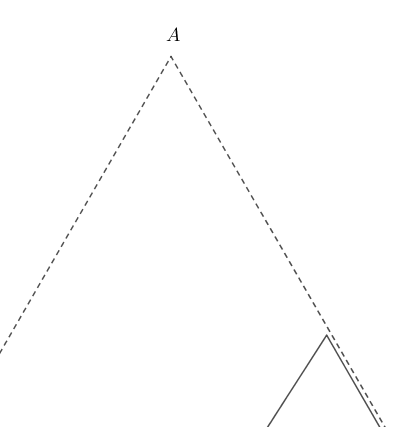
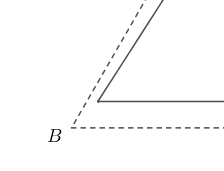
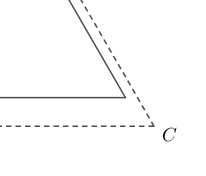
For more details on how the rotation is calculated, see the article Platonic Passages (Jerrard, Wetzel and Yuan, 2017). Note that I’ve used a different starting position for the tetrahedron, so the rotation is adjusted accordingly.

Sadly, the fit is so close that the edges of a tetrahedron with a suitable hole would be far too thin to 3D-print successfully. However, that doesn’t stop it being modelled and animated in OpenSCAD.

The Nieuwland constant of a polyhedron is the amount by which it can be scaled and still fit through a hole in the original-sized polyhedron. Under the conditions described above, a tetrahedron could be scaled by $\frac{2\sqrt{3}\left(\sqrt{6}-1\right)}{5}\approx\,1.004\,235$. This is currently the biggest known estimate for the Niewland constant of a tetrahedron, but it’s not proven to be the biggest.

The Geogebra and OpenSCAD files used to produce the images and animations in this article are available on GitHub.

Reference: Most of the information required to write this came from the article Platonic Passages (Jerrard, Wetzel and Yuan, 2017).