How many centres do you think a triangle has? There are more than you might think. Maybe you learned about a few at school – the centroid, incentre and circumcentre are the classic ones that most people learn. But there are a few (actually, more than a few) more than that.

One of them is called the nine point centre. As the name suggests, there are nine points involved in this centre.

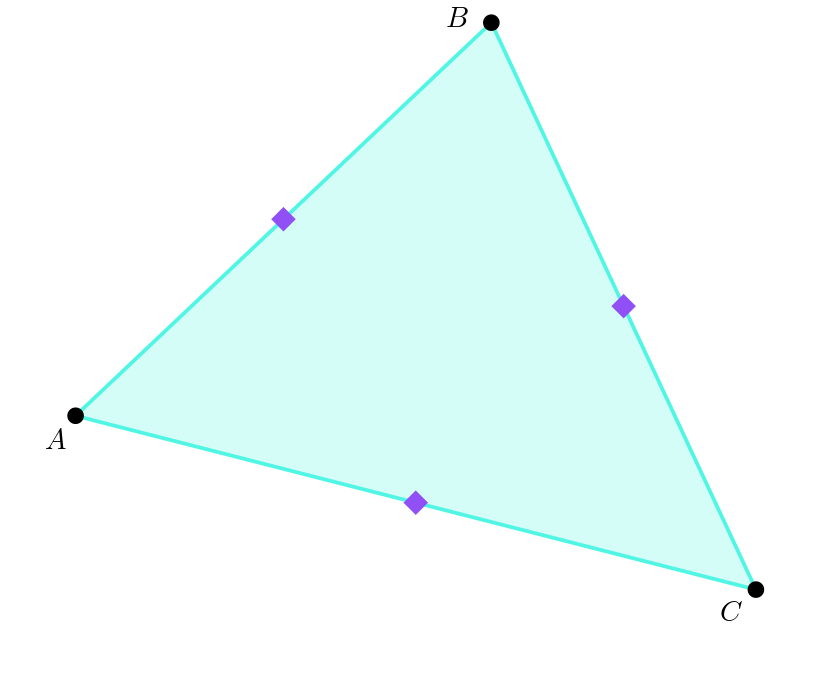
The first three are the midpoints of the sides: the points halfway between each pair of corners, shown here by the purple squares.

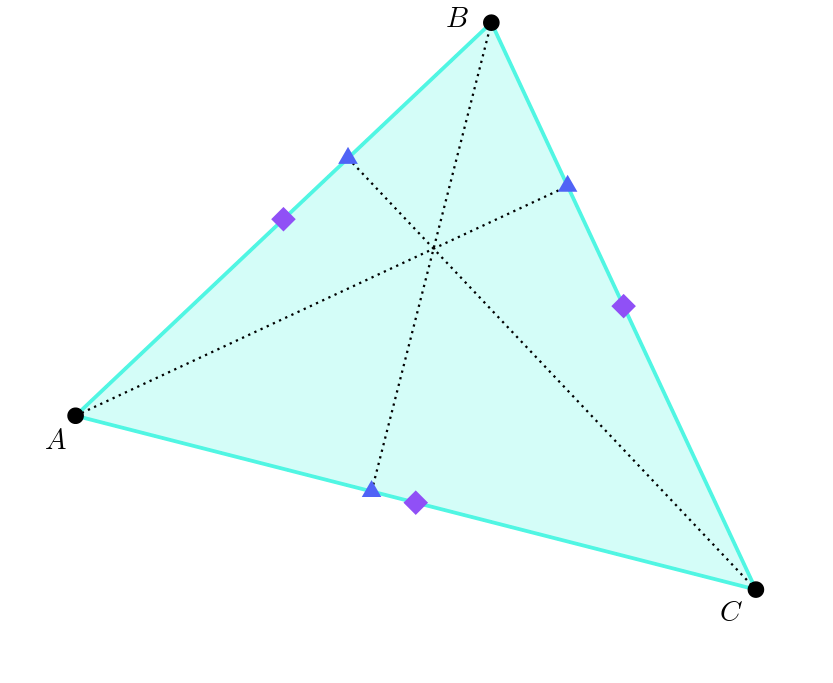
The next three are the altitude feet. An altitude is a line that goes through one corner and crosses the line through the other two corners at a right angle. The altitudes are shown here by dotted lines. The foot of an altitude (shown by blue triangles) is the point at which it crosses the line going through the other two corners. Sometimes the foot of an altitude is on a side of the triangle, sometimes it isn’t – it depends on the triangle.

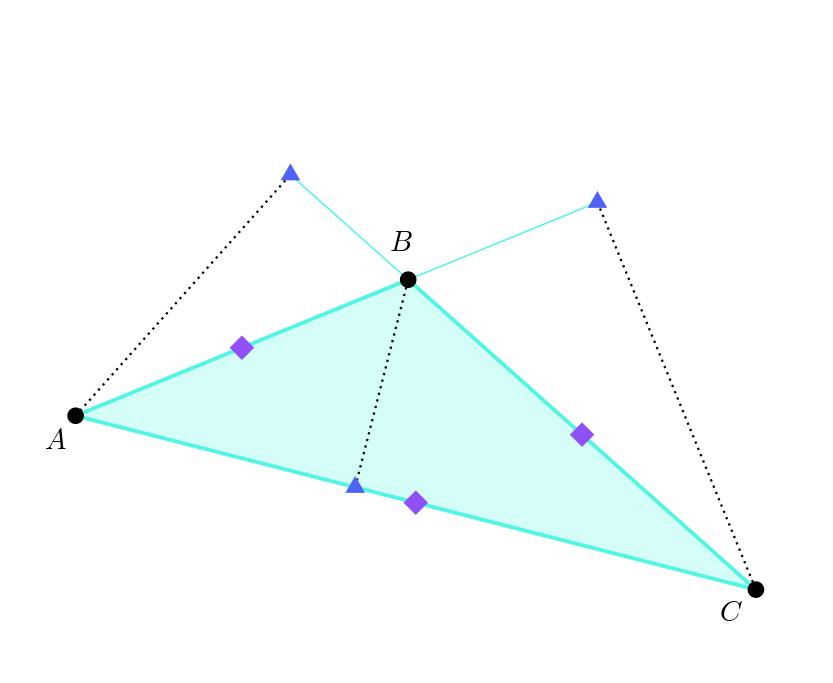
The three altitudes always meet at a single point, called the orthocentre (yes, yet another centre of a triangle). The final three points that we need for the nine point centre are the points halfway between the orthocentre and the corners of the triangle, shown by pink circles.

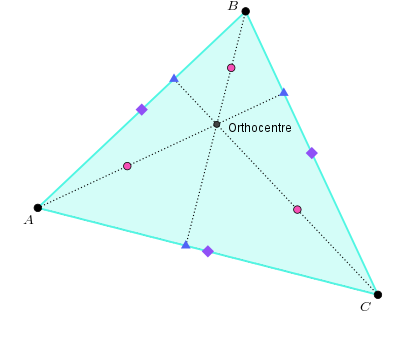
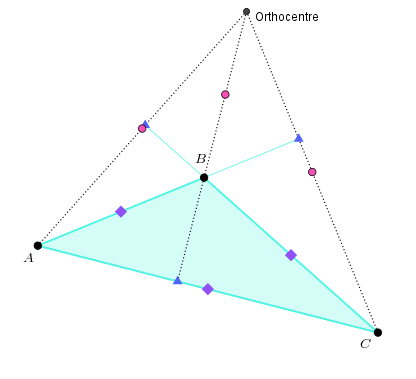
Look at the nine points on the two triangles. Do you notice any differences about how they’re positioned, or any similarities?

I notice that for the first triangle, all the points are either on a side of the triangle or inside it, whereas for the second triangle, two of the blue triangles and all the pink circles are outside the triangle. Also, each triangle has some points close together and some far apart – but not always the same points in each case.

As for similarities, for both triangles it looks as though all nine points lie on a circle – and in fact, that is true! It’s called the nine point circle, and the centre of this circle is the nine point centre.

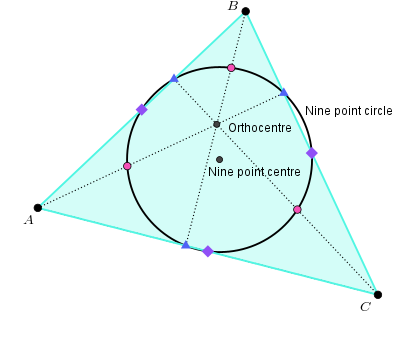
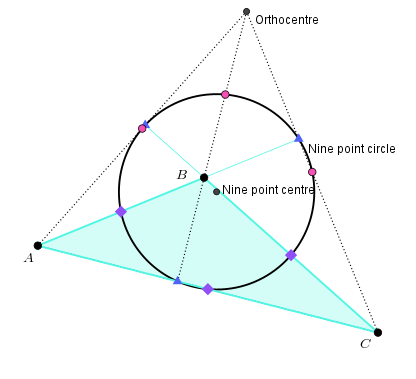
I find it astonishing that, whatever the shape of the triangle, these nine points always lie on a circle. You can test this out with the Geogebra applet below.

Some things to try:

• How far outside the triangle can you get the nine point centre?
• Can you get the orthocentre and the nine point centre to be in the same place?
• Which of the nine points can you get to be in the same place?