Imagine you’re a knight moving around on a chessboard, and you’re not allowed to visit any square that you’ve already been to. How quickly are you likely to get stuck?

Chess

First, some definitions. If you’re familiar with chess you can skip this section.

Chess is a two-player game played on a chessboard, which is an 8 by 8 grid of black and white squares.

A knight is one of the pieces used in a game of chess. It moves in an L-shape: two squares in one direction, followed by one square in another direction. So from any particular square, there are eight possible squares that a knight could move to (assuming that no move takes it off the edge of the board).

Knight’s tours

A knight’s tour is a path of knight’s moves that visits every square on the chessboard exactly once. There are billions of ways to do this! A few of them are shown below.

If you choose a square to start from and try making moves at random, how likely do you think it is that you’ll find such a path?

You can try this for yourself at https://maths-resources.com/knights/ – have a few tries and see how far around the board you can get before you get stuck.

Of course, you probably weren’t making truly random moves – you might have put some thought into which move was most likely to be successful. Even then, you’re pretty unlikely to have found a path all the way around. (If you did, congratulations!)

Randomly-generated knight’s moves

The graph below shows the results of one million attempts to find a knight’s tour by making moves at random. The number of squares visited is on the x-axis, and the number of times that was achieved is on the y-axis.

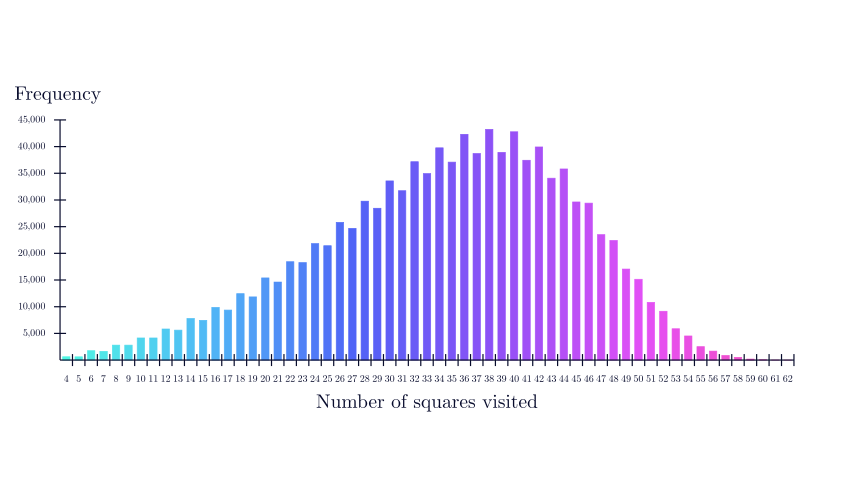
There are two striking things about this graph.

1: A full-length path (visiting all 64 squares) was never found.

In one million attempts, the longest path found visited only 62 of the 64 squares. Does this surprise you? To be honest, it didn’t surprise me very much. Although there are millions of paths that visit all 64 squares, there are millions more paths that don’t. The chance of getting all the way around the board by choosing random moves is very, very small.

2: There were some paths that only visited four squares.

This did surprise me! Four seems like a low number! Unless you were very unlucky, I expect you managed more than that when you tried it. This raises a question: where would you have to start from, and what moves would you have to make, to be stuck after only four moves?

If you like, you could go back to https://maths-resources.com/knights/ and see if you can work it out.

Or expand this section to see the answer.

One answer is shown below. Because of the symmetry in a chessboard there are seven other solutions, each starting one move away from a corner square and following a similar pattern.

More information

If you’ve enjoyed this article, you might also enjoy this video where I go into a little more detail, and sing a song about a knight looking for a knight’s tour.