#DigitalGeometrySketchbook Days 1 to 10

Throughout the month of June 2021 I created a daily maths art piece, each one using different software or different techniques, as part of the #GeometrySketchbook challenge on Twitter. As mine was all digital artwork, I used the #DigitalGeometrySketchbook tag. Here are the results of days 1 to 10.

Feel free to ask if you have questions about any of the techniques I’ve used. And if you’re inspired by any of these pieces, do let me know. I’d love to see what else you come up with! You can tweet me at @SamHartburn or email sam@samhartburn.co.uk.

Days 11 to 20

Days 21 to 30

1 June

Curve of pusuit animation, created in Scratch. Click on the green flag to start the animation, or look at the source file. I’ve usually created curves of pursuit using straight lines. In Scratch you can use the ‘point towards’ block to make each creature chase the next one, so these curves are from a literal pursuit. I would like to create some Scratch/MathsArt resources some day – there is so much potential there.

2 June

A Sierpinski triangle, created in Microsoft Word. I’m not a huge fan of Word’s drawing tools, but this was less frustrating than I expected it to be.

Sierpinski triangle in varying shades of blue. Dark in the centre and getting lighter in the corners.

3 June

A hexagon pattern made of impossible triangles, created in Geogebra. Geogebra is my goto app for maths art. You can see the source file here.

Seven hexagons, each formed of six impossible triangles in shades of blue.

4 June

A sunset, created using conditional formatting in Microsoft Excel. I was amazed by how good this looks! I created two ‘axes’ and populated the cells with the function $x^2+y^2$, then used one of the default conditional formatting options to colour it. You can download the source file from GitHub.

Red circle fading out to yellow, then fading to purple in the corners, with the aim of looking like a sunset.

5 June

Parabolic envelopes, created in Microsoft Paint. There was no point in trying to plot anything accurately in Paint, so I tried to embrace the lack of precision and just make a colourful sketch.

Sketchy parabolic envelopes in bright colours on a black background, using six spokes of different lengths and with different angles between them.

6 June

A pattern made of squares, circles and triangles, created in Inkscape. I tried to do something much more complicated than this, but it would have taken forever so I scaled it down a bit. I liked how easy it was to separate and colour the different sections of the pattern.

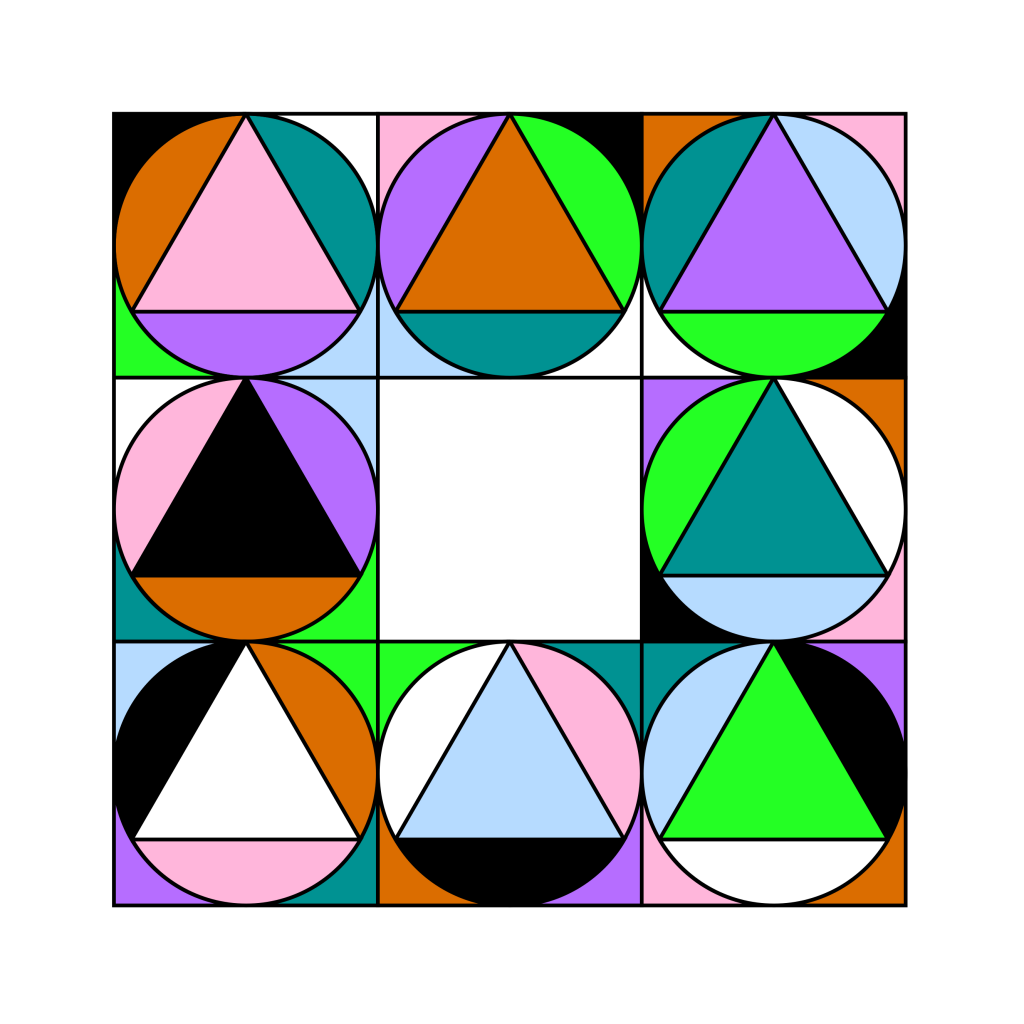
quare split into a 3 by 3 grid. Each of the outer squares contains a circle, which contains an equilateral triangle. Each section of each square is a different colour and the colours cycle around the sections in the same order, going clockwise. For example, the white section in a particular square is always black in the next square.

7 June

Seed of life, created in Geogebra and coloured in Gimp. This was inspired by a tweet from Paula Krieg. Gimp has some really fun brush effects, so I went a bit crazy! Like Inkscape, it’s easy to isolate and colour the different sections.

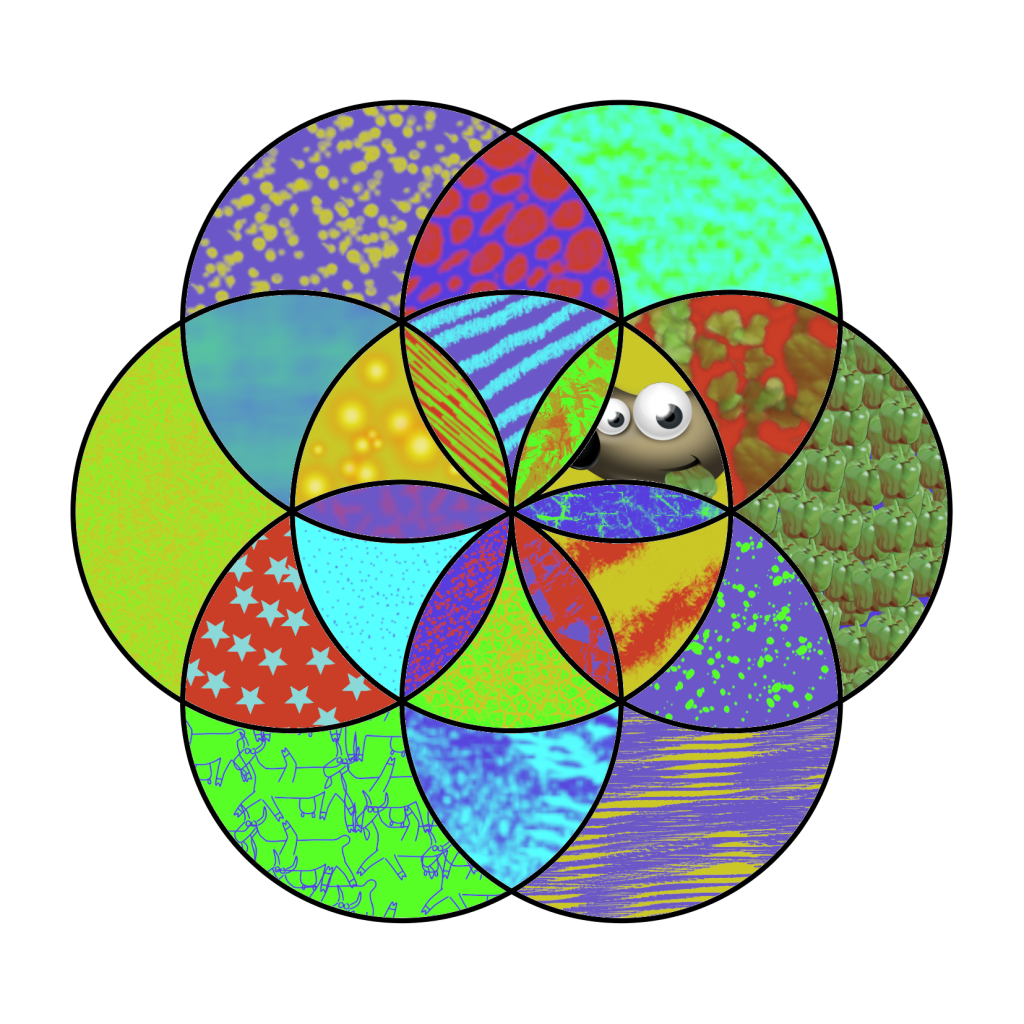
Flower of life made of 7 overlapping circles, each section coloured with a different colour combination/pattern.

8 June

More parabolic envelopes, created in Desmos. This was my first time using Desmos, and I was impressed by how straightforward it was. The list function is very intuitive. I liked seeing the extended lines of the envelopes and how they overlapped.

Four parabolic envelopes in the corners of a square, with all the lines continued in both directions, creating overlapping grids.

9 June

A pattern made from cubes, created in Mathigon’s Polypad. This was a dream to use! The pieces snapped into place beautifully. There’s loads of potential here to create cool geometric art.

Block structure made of blue, green and black rhombuses forming cubes.

10 June

Another Sierpinski triangle created in Microsoft Word, this time using Ascii art, inspired by Jim Cobb’s tweet. It’s Pascal’s triangle modulo 2, using . for 0 and w for 1 (because I thought it looked better!). You can download the source file from GitHub.

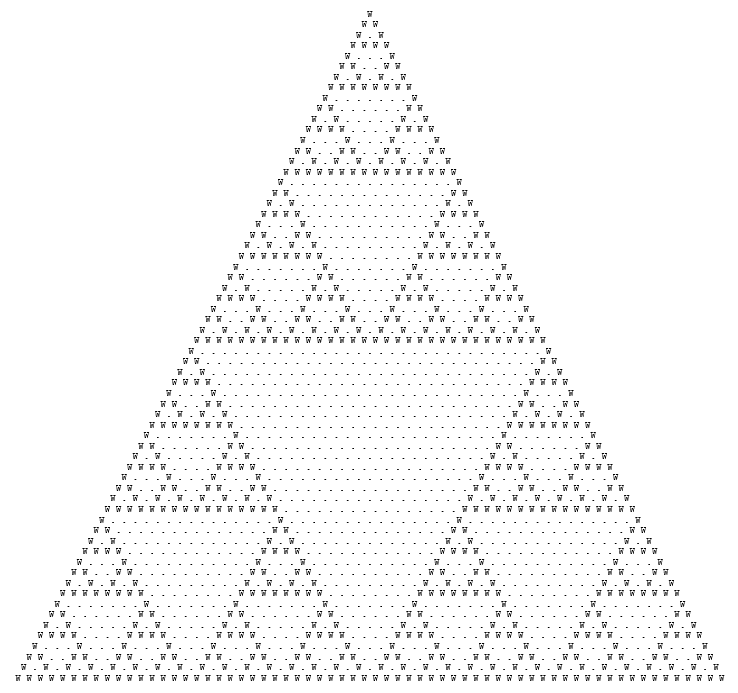
Sierpinski triangle made of full stops and letters w.

Sam Hartburn