For MathsJam 2019 I wrote a poem, (Not) Squaring the Circle, which features the construction of squares with the same area as given polygons. To make the poem work I had to omit some of the details of the constructions, and a few people have asked for more information about how they work. There is an explanation of the first part of the poem here. This post explains the second part of the poem, including how to construct squares with the same area as given triangles, pentagons and other polygons.

So, here we go
Oh
That’s a triangle

Never mind, I’ll give it a try
I can find the midpoint of any side
And draw a right angle up from there
It’s a crucial ingredient for a square

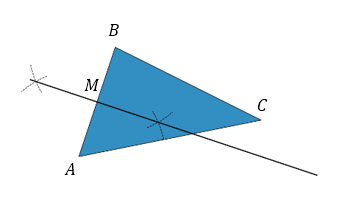
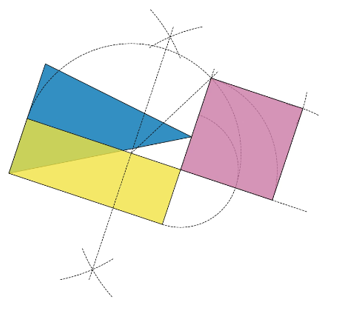
Hilariously, I now have a triangle instead of a circle. But I’m game for anything, so I’ll try to square it. Again, I’ve labelled the corners here to make it easier to refer back to them. The first step is to construct the perpendicular bisector of one side. It doesn’t matter which one – I’ve chosen $AB$. The midpoint is labelled $M$.

A parallel line through the third point now

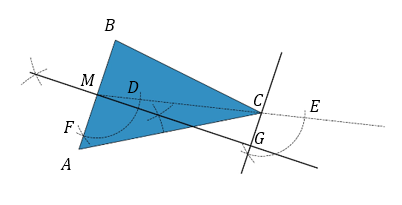
Next I construct a line parallel to $AB$, going through point $C$. To do this, I draw a line through $M$ and $C$, then copy angle $CMA$ at $C$. Draw two arcs of the same radius, one centered at $M$ and the other at $C$. Label the points of intersection with $MC$ as $D$ and $E$, and the point of intersection with $AB$ as $F$.

Now draw an arc centred at $D$, going through $F$. The radius of this arc is the crucial piece of information I need to copy the angle. Draw an arc of the same radius, centred at $E$, then draw a line going through both $C$ and the point where this new arc intersects the first arc. This line is parallel to $AB$. Label the point of intersection with the perpendicular bisector of $AB$ as $G$.

Fill in the top and the side somehow

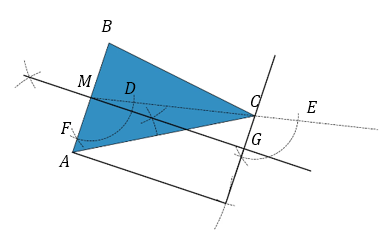
This isn’t very specific. The top and side of what? Well, so far I’ve constructed two sides of a rectangle. Now I need to construct the other two sides. I do this by drawing two arcs. The first has centre $G$ and radius $|AM|$, and the second has centre $A$ and radius $|MG|$.

It’s a rectangle, same height, half the base
And that means it takes up the same space

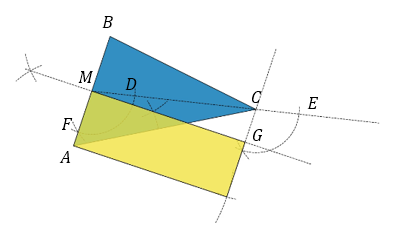
Now I have a rectangle with the same height as the triangle. Its other edge is half the length of the base of the triangle, so its area is $\frac{1}{2}\times\text{base}\times\text{height}$. But hang on, that’s the formula for the area of the triangle. So the rectangle and the triangle have the same area! This method was based on Euclid’s Elements, Book I, Proposition 42.

And I can already square a rectangle

As the poem states so succinctly, I can already square a rectangle (see Part 1).

But what about the circle?

So, here we go
Oh
That’s a pentagon

Never mind, I’ll give it a try

If I join the corners between pairs of sides
I can make it into triangles, one, two, three

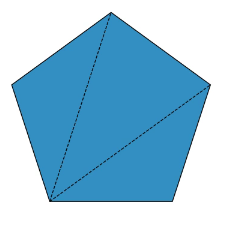
Oops, I still don’t have a circle – now I have a pentagon. I can divide a pentagon into triangles by choosing one corner and joining it to each of the other corners.

And squares from triangles are now easy

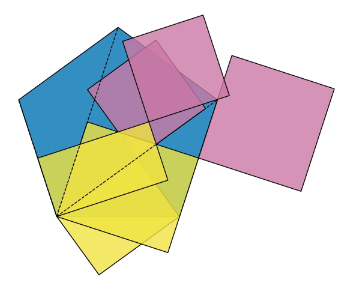
As shown above, I can construct a square with the same area as any given triangle. Now I have three squares, and the sum of their areas is equal to the area of the pentagon.

Put two sides together, joined at right angles
Then by some famous theorem involving triangles
The square on the long side sums the other two

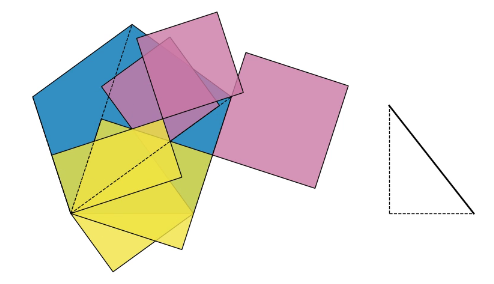
I can use the compass to copy the side lengths of two of the squares, putting them together at right angles. (Constructing a right angle is a standard ruler-and-compass construction, not shown here.) If I join the two loose ends to make a right-angled triangle then, by Pythagoras’ theorem, the area of a square drawn on this third side is equal to the sum of the areas of the first two squares.

Repeat the process, and then we’re through

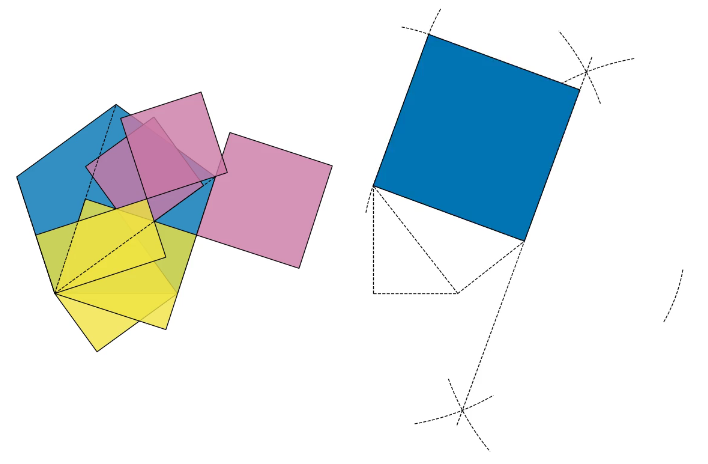
Now I can copy the side length of the third square and put it at right angles to the new length I just created. The hypotenuse of this right-angled triangle is the side length of a square with the same area as the pentagon, so all I have to do now is finish drawing the square.

But what about the circle?

So, here we go
Oh
That’s a hexagon

But come on, for six sides I know what to do
And the same will work for seven too
This is easy, look, it’s great
I can even do the same for eight
And nine, and ten, and –

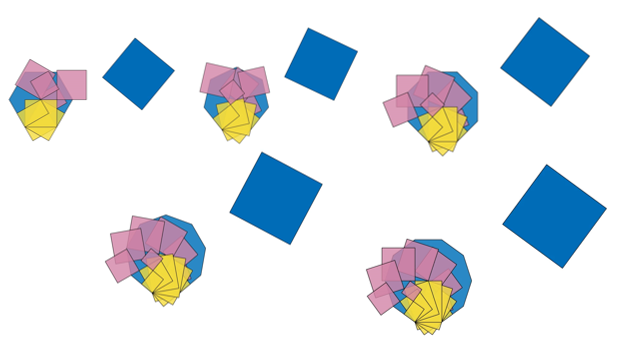
Suddenly everything is easy. I can divide any convex polygon into triangles, in the same way as I divided the pentagon, so now I have a method to construct a square with the same area as any given convex polygon.

holy cow!

That looks a bit like a circle now

But hang on. The more sides my polygon has, the more it looks like a circle.

In fact, I’ve got it, it’s obvious innit?
To square the circle, you take the limit!

So if I take the limit of this method as the number of sides tends to infinity, then I’ll have a method to square the circle. Won’t I?

The practical details of the construction
I’ll leave as an exercise for your deduction

Well, maybe not. If you want to try dividing a circle into an infinite number of triangles, be my guest. I think I’ll stick to polygons.