For MathsJam 2019 I wrote a poem, (Not) Squaring the Circle, which features the construction of squares with the same area as given polygons. To make the poem work I had to omit some of the details of the constructions, and a few people have asked for more information about how they work. So here is an explanation of the first part of the poem, including some background on the problem and details of how to construct a square with the same area as a given rectangle.

So I had this circle, but I wanted a square
Don’t ask why, that’s my affair
The crucial aspect of this little game
Is that the area should stay the same
Ruler and compass are the tools to use

Here I set up the problem. I’ve got a circle. I want to construct a square with the same area, using a ruler and compass. It’s an old problem, and for many centuries nobody knew if it was possible.

It’s been proven impossible, but that’s no excuse

In the early 1800s, Pierre Wantzel proved that it would be possible only if $\pi$ was an algebraic number. This means that it would have to be the root of a non-zero polynomial equation with rational coefficients. Later that century, Ferdinand von Lindemann proved that $\pi$ isn’t algebraic – it’s transcendental. This means that it has been proven impossible to construct a square with the same area as a given circle using only a ruler and compass.

Many have tried it, but hey, I’m me
I’m bound to find something that they couldn’t see

The fact that squaring the circle has been proven impossible hasn’t stopped people from trying to find a way to do it. Since Lindemann’s proof, many people have claimed to have found a method. Some of these may work to a certain number of decimal places, but, unsurprisingly, none offer an accurate method.

So, here we go
Oh
That’s a rectangle

Never mind, I’ll give it a try
Call the long edge x and the short edge y

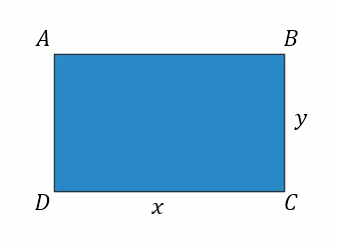
For a reason that is never explained, I find myself with a rectangle instead of a circle. I decide to have a go at squaring it, starting by labelling the edges so that I can refer back to them later. Here I’ve also labelled the corners.

Now make an arc to find y + x

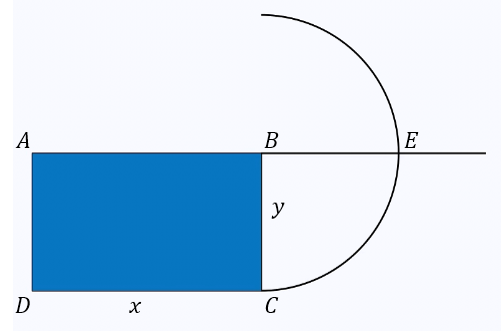
With the compass point on $B$, draw an arc of radius $y$. With the ruler, extend edge $AB$ until it meets the circle. Label the point of intersection $E$. The length $|AE|$ is $y + x$.

From the midpoint, make a semicircle next

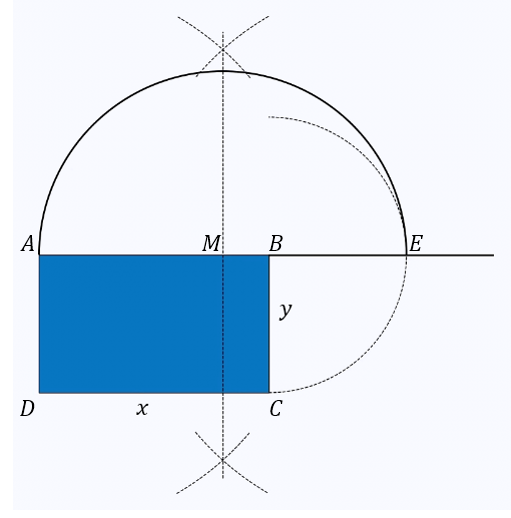
Construct the perpendicular bisector of $AE$ to find the midpoint, and label the midpoint $M$. With the compass point on $M$, draw a semicircle of radius $ME$.

Extending y to that arc gives the length I desire

With the ruler, extend edge $CB$ to meet the semicircle. Label the point of intersection $F$. The length $|BF|$ is the side length of the square that will have the same area as the rectangle.

I can prove it with algebra if you require

Now I need to prove that this is the correct length. To do this, I draw an extra line from $M$ to $F$, creating a right-angled triangle. This line isn’t needed for the construction, it’s just to prove that the construction is correct. I know that $|MF|=\frac{x+y}{2}$ by construction. I can calculate $|MB|$:

$\begin{align}
|MB|&=|AE|-|AM|-|BE|\\
&=x+y-\frac{x+y}{2}-y\\
&=\frac{x+y}{2}-y\\
&=\frac{x+y-2y}{2}\\
&=\frac{x-y}{2}
\end{align}$

By Pythagoras’ theorem,

$\begin{align}
|FB|^2&=|MF|^2-|MB|^2\\
&=\left( \frac{x+y}{2} \right)^2- \left( \frac{x-y}{2} \right)^2 \\
&= \frac{x^2+2xy+y^2}{4} – \frac{x^2-2xy+y^2}{4} \\
&= \frac{4xy}{4} \\
|FB|&=\sqrt{xy}
\end{align}$

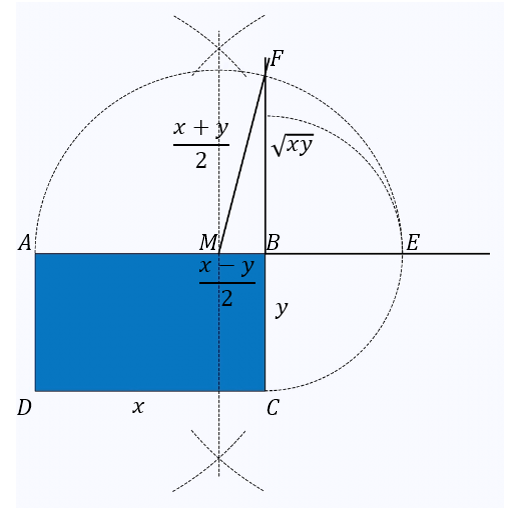
So the area of a square of side length $|FB|$ is $\left(\sqrt{xy}\right)^2=xy$, which is the same as the area of the rectangle.

Draw a square on that side,

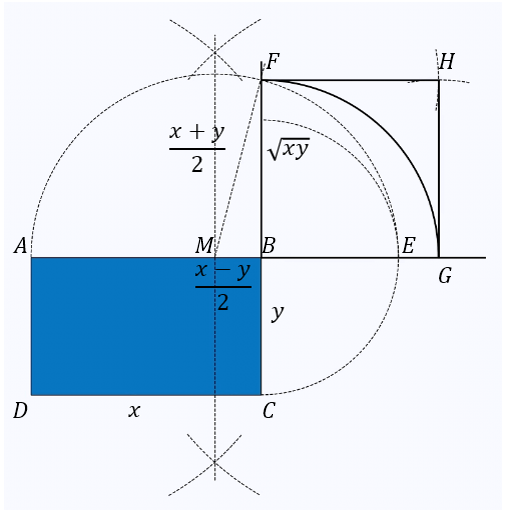
I already have a right angle at $B$, so I can draw an arc with centre $B$ and radius $|FB|$ to find the third corner of the square, where the arc crosses $BE$. Call this point $G$. To find the fourth corner, draw two arcs of radius $|FB|$, centred at $F$ and $G$. The point where they cross gives the fourth corner of the square, $H$.

and I don’t want hysteria

But the square and the rectangle have the same area

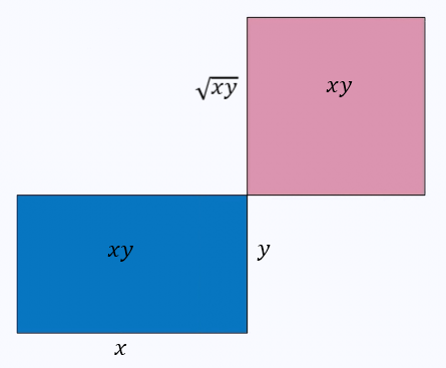
It is exciting, but try to keep calm. As already shown above, the square and the rectangle both have area $xy$. The method used here was based on Euclid’s Elements, Book II, Proposition 14.

But what about the circle?

Squaring the rectangle was fun, but it’s not what I set out to do. Look out for future parts where I’ll explain how to construct squares with the same area as given triangles, pentagons and more. And maybe even circles.*

21 Dec 2019: There is now an explanation of the second part of the poem here.

* Not circles. Really, it’s impossible.