And what does that have to do with maths?

A little while ago, Abs Pascoe (who I highly recommend if you’re thinking of starting singing lessons and you happen to live near Whitstable) posted this amazing video where she sings two different notes at once. I had never heard anything like it before! My first thought was that it was some kind of dark magic. My second thought was that there must be some interesting maths going on there.

I’m going to give a brief summary of what I understand about how it works. I found most of the information at Voice Science Works, and I recommend visiting that site if you want all the glorious technical details.

When a person sings, the sound is made by the vocal folds vibrating. The pitch of the note depends on the frequency of the vibration; a faster vibration produces a higher pitch. But the vocal folds vibrate at more than one frequency at once (as does almost anything that vibrates). The lowest frequency is called the fundamental; this is the main note you hear when somebody sings. The higher frequencies are called harmonics. The frequencies of the harmonics are all integer multiples of the frequency of the fundamental – the first harmonic is twice as fast, the second is three times as fast, and so on. The harmonics also produce sounds, called overtones, but they’re higher and quieter than the fundamental. You usually hear them all together as one sound.

The fundamental and harmonics can be represented by sine waves. If we start with the fundamental function $y=\sin(x)$, we can find the functions of the overtones by multiplying $x$ by 1, 2, 3, and so on. The diagram below shows the initial sine wave, representing the fundamental pitch, and the first nine overtones. You can see that the curves all start and finish at the same place, and they all go through the same point in the centre. If you look closely, you can see that there’s one wave that goes up and down only once – that’s the fundamental. Then there’s a wave that goes up and down twice – that’s the first overtone. After that it becomes harder to follow the curves.

So far, so messy. But that’s not really accurate. The fundamental is much louder than the overtones. We can represent this by increasing the amplitude of the initial sine wave; I’ll also make it thicker.

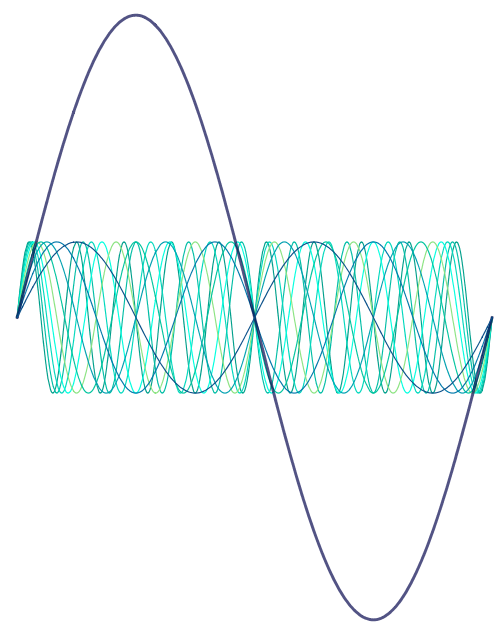
Now we can clearly see the fundamental; the overtones are just there in the background. But what does this have to do with singing two notes at once?

Another key part of the voice is the vocal tract. This is a space of air that goes from the vocal folds all the way up to the lips. When a person sings the air in the vocal tract vibrates, amplifying the sound produced by the vocal folds.

Here’s where the magic comes. The resonant frequency of the vocal tract changes depending on its shape and size. If the resonant frequency matches that of one of the overtones, that overtone will be massively amplified over the others, so suddenly it can be heard alongside the fundamental. That’s what’s happening in Abs’s video – she’s changing the shape of her vocal tract to amplify one overtone after another. Viewed as sine waves, it’s something like the following.

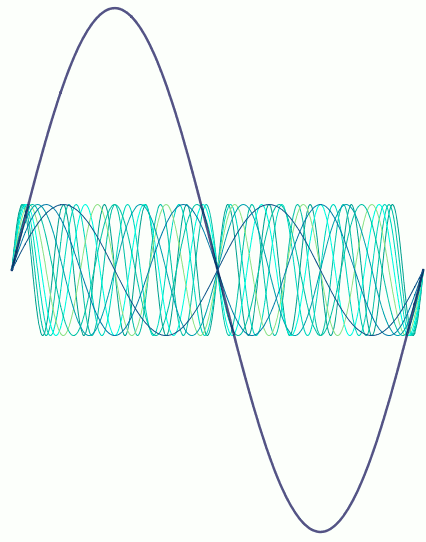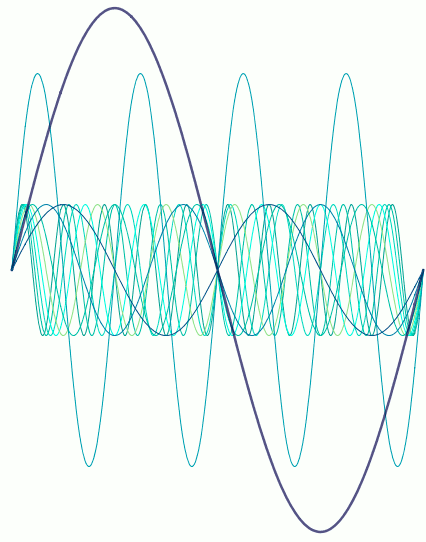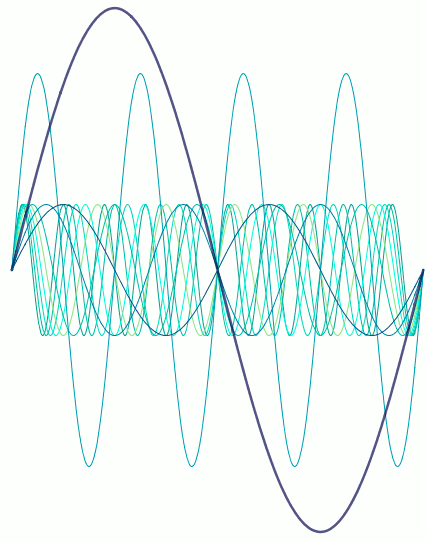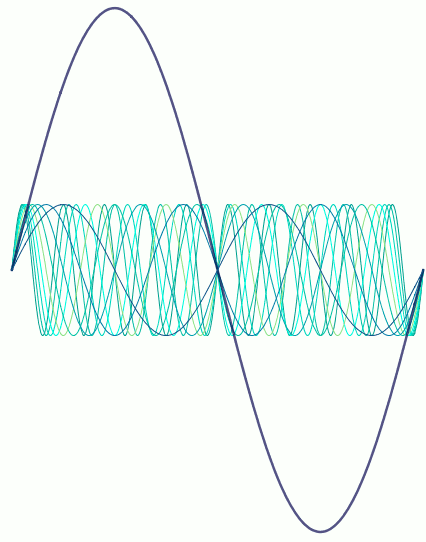
So there was some interesting maths going on! Although I still maintain that having that level of control over your voice must involve magic. Either that, or years of training and experience – but that’s much harder to achieve.