I recently found out about a shape I’d never heard of before: a chiliagon.

A chiliagon is a polygon (a shape made of straight edges) with 1000 sides. In a regular chiliagon, where all the sides are the same length and all the angles are the same size, the angle between two sides is roughly 179.64$^\circ$, so two adjacent sides are very close to being a straight line.

The image below shows a straight line, and an angle of 179.64$^\circ$ sitting on top of it. One side of the angle lies along the straight line, the other doesn’t. Can you tell the difference?

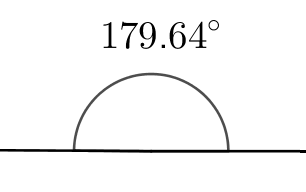
What if the lines are longer?

Now there’s a clear gap on the left-hand side. The further away from the point of the angle you travel, the bigger the gap will get. So just because two things look the same from a particular viewpoint, it doesn’t mean that they are the same.

The next image shows a regular chiliagon – a shape made up of 1000 straight lines. Judge for yourself: is it the same as a circle? If so, why? If not, why not?

There’s another way of looking at the chiliagon that might affect your answer. In the next image I’ve added lines from the centre point of the chiliagon to each of the corners. There are 1000 of them.

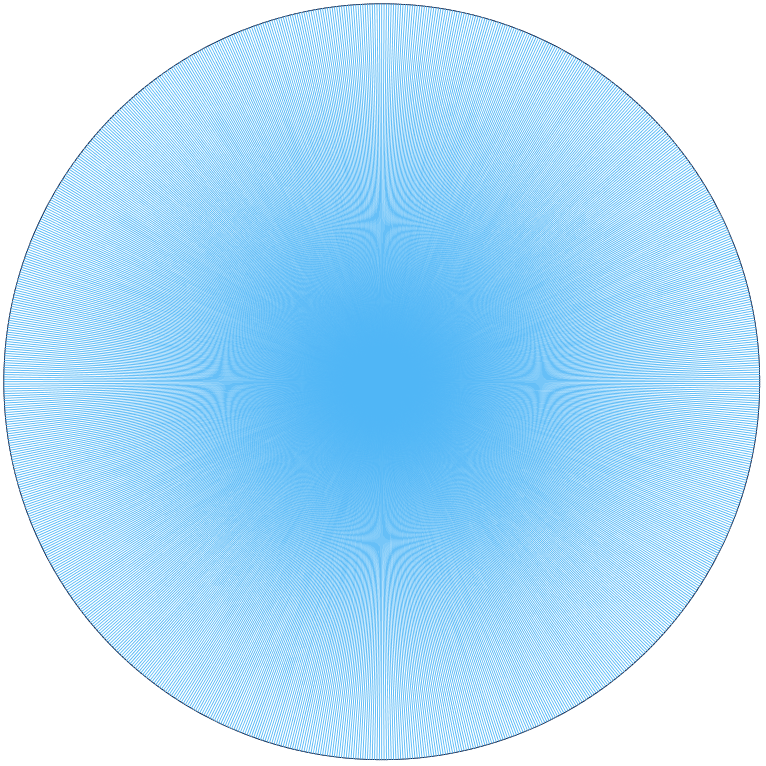
Does this change your answer? What would it look like if we carried out this process on a circle? Is it even possible to do that?

When you looked at the last image, you might have thought that it doesn’t look like the chiliagon is filled with straight lines. Maybe you can see strange curves and patterns. These are interference patterns caused by the lines being so close together – it’s called a moiré effect. You can play with it in the Geogebra applet below by dragging the slider to change the number of sides. How do the moiré patterns change as you change the number of sides? When does the shape stop looking like a circle?

Have fun!